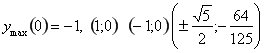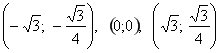Самостійна робота № 12
Дослідження функції, побудова її графіка.
Список літератури:
- М. В. Грисенко «Математика для економістів: Методи й моделі, прик- лади й задачі.»: Навч. Посібник. – К.:Либідь, 2007., (ст. 323 – 335)
- К.Г. Валлєєв, І.А. Джалладова “Вища математика”, навч.посібник К.: КНЕУ, 2002.,(ст. 434-471)
- К.Г. Валлєєв, І.А. Джалладова та ін. “Вища математика”: Навчально-методичний посібник для самостійного вивчення дисципліни. – К.: КНЕУ, 2002. (ст. 221-236)
- Михайленко В.М., Федоренко Н.Д. Алгебра та геометрія для економістів – К.: Українсько-фінський інститут менеджменту і бізнесу, 1997 (ст. 74-91)
- В.Г. Лісічкін, І.Л. Соловейчик . Математика: Навчальний посібник для технікумів – М.: Вища школа, 1991 (ст.255-286).
Питання, які необхідно опрацювати
- Зростання та спадання функції.
- Екстремуми функцій.
- Найбільше та найменше значення функцій на відрізку.
- Опуклість і вгнутість функції. Точки перегину.
- Асимптоти.
- Загальний план дослідження функцій і побудова їхніх графіків.
Контрольні питання
- Яка необхідна і достатня умови існування екстремумів?
- Як дослідити функцію на екстремум за допомогою першої та другої похідної?
- Яке правило дослідження функції на опуклість, вгнутість та точки перегину.
- Які є асимптоти?
- Як дослідити функцію на наявність похилої асимптоти?
- Як дослідити функцію на наявність горизонтальної асимптоти?
- Як дослідити функцію на наявність вертикальної асимптоти?
- Яка загальна схема дослідження функції?
Завдання для самостійної роботи
Дослідити функції та побудувати їх графіки:
Рівень І.
1. 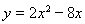 2. 2.  3. 3. 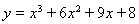 4. 4. 
Рівень ІІ.
5.  6. 6. 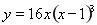 7. 7. 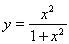 8. 8. 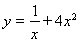
Рівень ІІІ.
9. 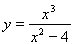 10. 10.  11. 11. 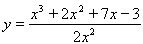 12. 12. 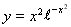 . .
Відповіді
1.  . Ні парна ні непарна. (0;0) (4;0); . Ні парна ні непарна. (0;0) (4;0); 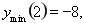 точок перетину немає. Асимптот немає. точок перетину немає. Асимптот немає.
2.  . Ні парна ні непарна. (0;0) (4;0); . Ні парна ні непарна. (0;0) (4;0); 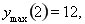 точок перетину немає. Асимптот немає. точок перетину немає. Асимптот немає.
3.  . Ні парна ні непарна. (0;0) (4;0); . Ні парна ні непарна. (0;0) (4;0);  Асимптот немає. Асимптот немає.
4.  . Графік симетричний відносно осі ординат. . Графік симетричний відносно осі ординат. 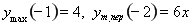 Асимптот немає. Асимптот немає.
5.  . Графік симетричний відносно осі ординат. . Графік симетричний відносно осі ординат. 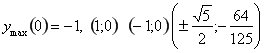 - точки перегину. Асимптот немає. - точки перегину. Асимптот немає.
6.  . Ні парна ні непарна. . Ні парна ні непарна. 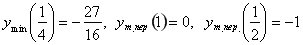 Асимптот немає. Асимптот немає.
7.  Графік симетричний відносно початку координат Графік симетричний відносно початку координат 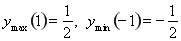 . Точки перегину . Точки перегину 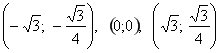 . Асимптота . Асимптота  . .
8. 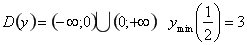 . Точка перегину . Точка перегину  . Асимптота х=0. . Асимптота х=0.
9. 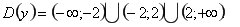 . Функція непарна. Графік проходить через початок координат. На інтервалі (-2;2) монотонно спадає. . Функція непарна. Графік проходить через початок координат. На інтервалі (-2;2) монотонно спадає. 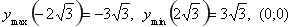 - точка перегину. На інтервалах - точка перегину. На інтервалах  графік опуклий, на графік опуклий, на  угнутий. Асимптоти угнутий. Асимптоти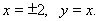
10. 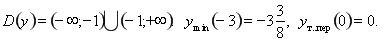 Асимптоти х=-1 та Асимптоти х=-1 та 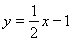 . .
11.  . Абсциса точки перегину . Абсциса точки перегину 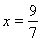 . Асимптоти х=0, . Асимптоти х=0, 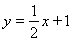 . .
12.  . Функція парна. . Функція парна. 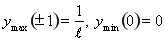 . Абсциси точок перегину графіка функції . Абсциси точок перегину графіка функції  . Асимптота . Асимптота 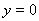 . .
|