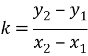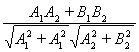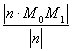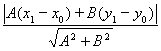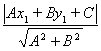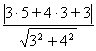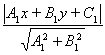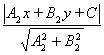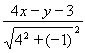3. Рівняння прямої, що проходить через дві дані точки.

Нехай дано дві різні точки М1(х1;у1), М2 (х2,у2), де х2 ≠ x1. З рі­вняння (2) випливає вираз для кутового коефіцієнта прямої, що проходить через точки М1, М2:        (3)

Підставляючи в (3) рівняння (2) знаходимо рівняння прямої, що проходить через дві задані точки М(x;y), M(x;y):     =    (4)

Приклад. Знайдемо рівняння прямої, що проходить через дві задані точки М(4;1), M2(2;3).

Згідно з (4) маємо:

           = ,    y = − x + 5.

4. Рівняння прямої , яка проходить через дану точку  і має заданий направляючий вектор.

Якщо задано вектор паралельній деякій прямій, і точку на цій прямій, то рівняння прямої можна записати у вигляді:     

5.  Рівняння прямої у відрізках.

       Щоб побудувати графік прямої, достатньо дві її різні точки і через них провести пряму. Якщо пряма перетинає осі координат у точках М1(а;0), М2(0;b), а ≠ 0, b ≠ 0, то її можна записати рівнянням

(5)

яке називається рівнянням прямої у відрізках на осях

   Приклад. Запишемо рівняння прямої

y = −x + 2

у вигляді (5).

   • Значенню y1 = 0 відповідає x1 = 3. При х2 = 0 знаходимо у2 = 2. Отже, шукане рівняння прямої подається у вигляді

                                                     +=1

        Пряма перетинає вісь х у точці з координатою х = 3, а вісь у — у точці з координатою у = 2.

6. Взаємне розміщення двох прямих.

Дві прямі задано їх загальними рівняннями:

A1x+B1 y + C1 = 0 ,   А2х + В2у+С2=0.    (1)

Точку перетину М(х, у) цих прямих знаходимо, розв'язуючи систему рівнянь, оскільки координати х, у точки М задоволь­няють одночасно обидва ці рівняння.

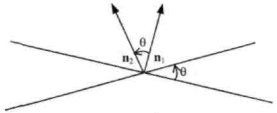
Кут між даними прямими дорівнює куту між їх нормалями n1 = (A1; B 1),

n2= (A2, В2), (рис. 4).

                 Рис. 4

Отже, маємо такі залежності:

=     —    умова паралельності прямих.         (2)

Якщо прямі збігаються, то їх коефіцієнти пропорційні:

                 =  =     —    умова перпендикулярності прямих.       (3)

Скориставшись формулою скалярного добутку векторів, знай­демо кут :

cos =.    (4)

7. Відстань від точки  до прямої

Дано загальне рівняння прямої

Ах + Ву + С = 0   (1)

і точку М1(х1, у1). Знайдемо відстань d від точки М1 до прямої (1). Візьмемо точку М0(х0 У0) на цій прямій.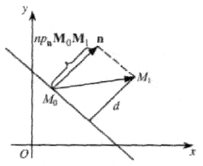

Тоді відстань від точки М1 до прямої дорівнює проекції вектоpa M0M1 на вектор нормалі n = (A, В) (рис. 5).

Записуємо аналітичний вираз для шуканої відстані:

     d = = =

Оскільки – Ах0 – Ву0 = С, то остаточно маємо:     d =       (2)

Означення. Рівняння виду     = 0       (3)

називається нормальним рівнянням прямої (1). Знак перед радикалом має бути протилежний знаку вільного члена С. Якщо С = 0, то вибір знака значення не має.

  Приклад.   Обчислити відстань d від точки М1(5, 3) до прямої 3х+ 4у + 3 = 0.

За формулою (2) знаходимо    d = = 6.

Нехай маємо загальні рівняння двох прямих, що перетинаються:

                                  А1х + Ву1 + С1=0,   А2х + В2у + С2=0.         (4)

Якщо точка М(х, у) лежить на бісектрисі кутів, утворених прямими (4), то вона однаково віддалена від цих прямих, тобто виконується рівність:

=            (5)

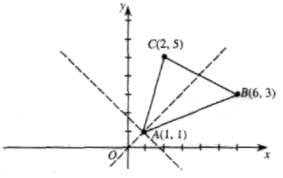
Приклад: Знайти рівняння бісектриси AD трикутника з вершинам А(1, 1), В(6, 3). С(2, 5) (рис. 6).

Згідно з (5) записуємо рівняння двох бісектрис:

=. Звідси маємо: − = 0  (6)

або     = 0              (7)

Ці прямі на рис. 6 зображено пунктиром. Вони взаємно перпен­дикулярні. Щоб знайти бісектрису трикутника ABC, підставимо коор­динати точок В(6, 3), С(2, 5) у рівняння (6) і (7). Оскільки точки В, С лежать по різні боки від шуканої бісектриси, то в результаті підстав­ляння координат точок 5(6, 3), С(2, 5) у зазначені рівняння дістанемо числа різних знаків.

Справді, для рівняння (6) маємо:

                     − <0, − <0

                                               (числа однакових знаків);

для рівняння (7):

+>0, +<0

(числа різних знаків).

Отже, рівняння (7) визначає шукану бісектрису трикутника ABC.