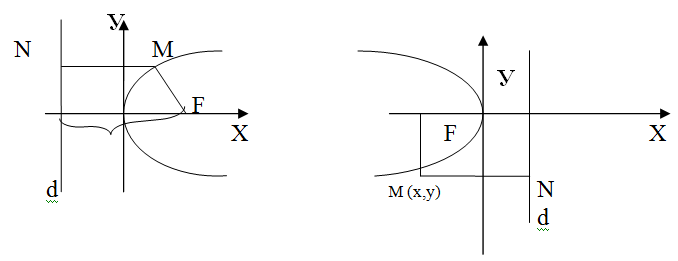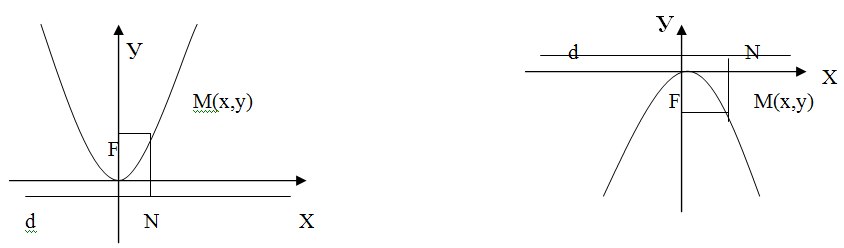4. Гіпербола та її канонічне рівняння.

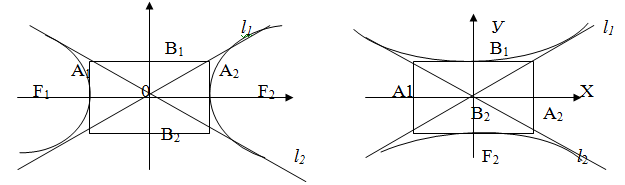
Гіперболою називають геометричне місце точок площини, модуль різниці відстаней кожної з яких до двох даних точок, які називають фокусами, величина стала і менша за відстань між фокусами.

F1 і F2 - фокуси

2с – відстань між фокусами

2а – різниця відстаней від б-я точки гіперболи до її фокусів.

Канонічне рівняння гіперболи           або

де а, b, с зв’язані між собою рівностями .

Два основних випадки розташування гіперболи відносно осей координат:

Розташування фокусів           F1 і F2  ОХ                 F1 і F2  ОУ

Координати фокусів          F1 (-с; 0) і F2 (с;0)            F1 (0; с) і F2 (0;-с)

Дійсна вісь                                                     

Уявна вісь                                                      

Фокусна віддаль                                             

Ексцентриситет                                                     

Співвідношення між а, b, с                                      

Рівняння                                                       

Ексцентриситетом гіперболи називають відношення відстані між фокусами до довжини дійсної вісі.

Прямі l1 і l2- асимптоти і їх рівняння мають відповідно вигляд 

l1: ;                         l2: .

Гіпербола у якої довжина уявної вісі дорівнює довжині дійсної вісі називається рівносторонньою.

Якщо F1 і F2  ОХ і а=b то рівняння гіперболи прийме вигляд   

Якщо F1 і F2  ОУ і а=b то рівняння гіперболи:       

Для рівносторонньої гіперболи справедлива рівність: .

Бо  ,   звідки  .

Рівняння асимптоти   l1: ;   l2: .

Приклад 3.

Скласти рівняння гіперболи з фокусами на осі ОХ, якщо її дійсна вісь рівна 16, а уявна  8.

Розв’язання:

Оскільки по умові задачі , то рівняння гіперболи .

Так як 2а=16,  а=8,     2b=8 , b=4. Підставивши отримані дані в загальну формулу, отримаємо: .                                       

Приклад 4.

Знайти координати фокусів, довжину осей, ексцентриситет і асимптоти гіперболи, заданої рівнянням .

Розв’язання:

Зведемо дане рівняння до канонічного вигляду:     .

З рівняння видно, що F1 і F2  ОХ, отже

,    а=5,    дійсна вісь 2а=10;          ,   b=3,  уявна вісь 2b=6.

Рівняння асимптот: .

Із співвідношення між a, b та с:  с2==25+9=34 , звідки  с=.

Отже фокуси

Ексцентриситет для  I-го випадку .      

Приклад 5.

Скласти рівняння рівносторонньої гіперболи, що проходить через точку М (-10, 8). F1,F2  ОХ.

Розв’язання:

Так як точка М належить рівносторонній гіперболі у якої , то її координати задовольняють канонічне рівняння . Знайдемо , підставивши координати точки М в дане рівняння: .

Отже, - шукане рівняння.

 5. Парабола та її канонічне рівняння.

Параболою називають геометричне місце точок площини, рівновіддалених від заданої точки, що називається фокусом і даної прямої, що називається директрисою.

Фокус позначають буквою F, директрису - буквою d.

Відстань від фокуса до директриси Р.

Розглянемо основні випадки розташування параболи відносно осей координат.

Парабола коли :

Положення фокуса         на додатній півосі ОХ            на від'ємній півосі ОХ

Координати фокуса                                                

Рівняння директриси                                                  

Канонічне рівняння                                                                                         

Парабола коли :

Положення фокуса          на додатній півосі ОУ                     на від'ємній півосі ОУ

Координати фокуса                                                   

Рівняння директриси                                                   

Канонічне рівняння                                                      

 Приклад 6.

Знайти координати фокусів і рівняння директриси параболи, заданої рівнянням .

Розв’язання:

Даному рівнянню відповідає канонічне рівняння для якого координати фокуса  і рівняння директриси  .  Отже, потрібно знайти величину .

Знайдемо її з рівності:    ,    ,   . Підставивши отримане значення у формули, будемо мати:       .                       

Приклад 7.

        Скласти канонічне рівняння параболи і рівняння її  директриси з вершиною в початку координат і фокусом  .

Розв’язання:

    Оскільки, фокус задовольняє формулу, то  , звідки . По координатах фокуса ми бачимо, що він належить від'ємній півосі ОУ. Тому  канонічне рівняння параболи і рівняння її директриси для даного випадку відповідно є: і  . Підставляючи отримане значення в ці рівняння, будемо мати:      

Приклад 8.

Скласти канонічне рівняння параболи симетричної відносно осі OX  з вершиною в початку координат, що проходить через точку С(- 3; - 9).

Розв’язання:

      Оскільки, парабола симетрична відносно осі OX  то це або 1-й, або 2-й випадки. А оскільки вона проходить через точку С, що належить IV чверті , то це буде 2-й випадок, якому відповідає рівняння . Підставивши у нього координати точки С, знайдемо величину : ,           Отримане значення підставляємо у відповідне канонічне рівняння: .