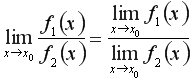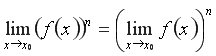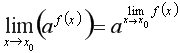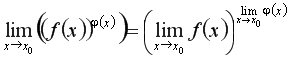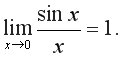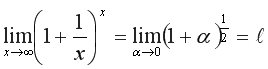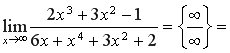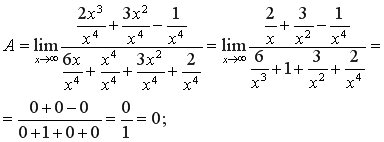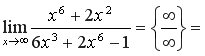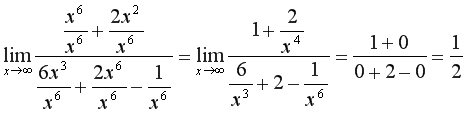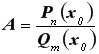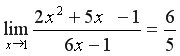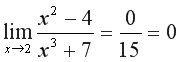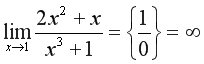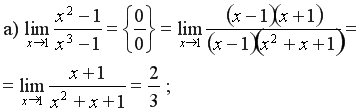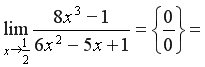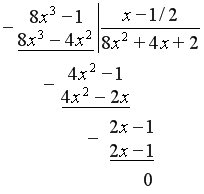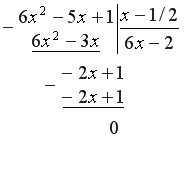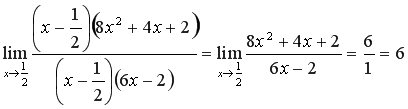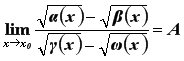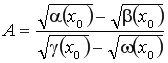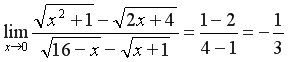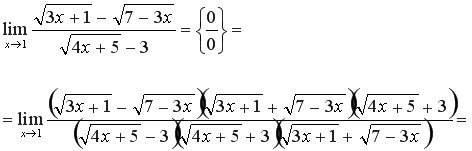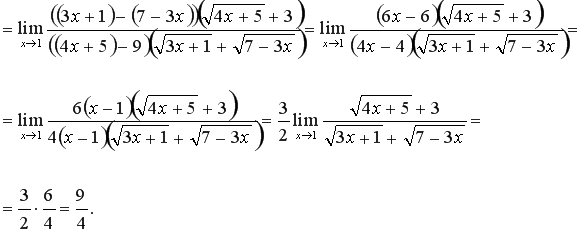ГРАНИЦЯ ФУНКЦІЇ

 

          Нехай функція визначена у точці і деякому околі цієї точки. Число називається границею функції  при , якщо тобто .

 

Основні теореми про границі

1. Сталий множник можна виносити за знак границі:

.

2. Границя суми функцій дорівнює сумі границь:

.

3. Границя добутку функцій дорівнює добуткові границь:

.

4. Якщо існують і , то

.

 

Теореми про граничний перехід

1. Границю можна вносити під знак степеня:

.

2. Логарифм і границю можна міняти місцями:

.

3. Границю можна вносити до показника степеня:

.

4. І узагальнення: .

Чудові границі.

1.            2. .

Розглянемо декілька методів знаходження границь функцій.

 

Почнемо з границі відношення двох многочленів при :

.

Для знаходження границі чисельник і знаменник почленно ділимо на найстарший степінь та використовуємо основні теореми.

Приклад 1

а) А.

Треба поділити почленно чисельник і знаменник на :

б) А.

Для того щоб знайти границю, необхідно почленно поділити чисельник і знаменник на старший степінь , тобто на :

А = .

 

Розглянемо границю відношення двох многочленів при

.

 

Можливі такі випадки:

      1. і . Тоді .

Приклад 2

.

 

      2. і . Тоді .

Приклад 3

.

 

      3. і . Тоді .

Приклад 4

.

 

 

4. і . Тоді маємо невизначеність типу .

Для того щоб знайти границю у цьому випадку, необхідно і в чисельнику, і в знаменнику виділити множники , де - кратність кореня, а далі скоротити на цей множник.

 

Приклад 5

.

б) А.

Для того щоб розкласти на множники, розділимо чисельник і знаменник на :

     

А = .

 

Розглянемо границю відношення двох виразів, які мають квадратні корені при :  .

 

Можливі кілька випадків:

      1. і , тоді границя

           знаходиться зразу .

Приклад 6

.

 

      2. , а , тоді .

 

      3., а , тоді .

 

      4. і , тоді маємо невизначеність типу .

Щоб її розкрити, необхідно домножити чисельник і знаменник дробу на спряжені вирази і для чисельника, і для знаменника для того, щоб звільнитися від квадратних коренів. А потім виділити і в чисельнику, і в знаменнику множник та скоротити на цей множник.

Нагадаємо, що .

 

Приклад 7