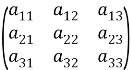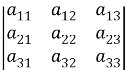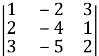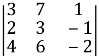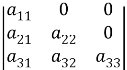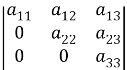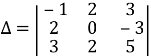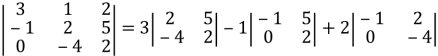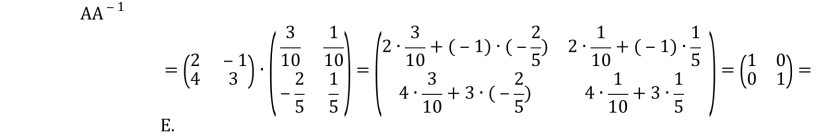Лекція  2

Визначники.

План.

1.                     Визначники. Обчислення визначників другого та третього порядків.
2.                     Властивості визначників.
3.                     Мінори та алгебраїчні доповнення.
4.                     Теорема про розклад визначника по елементах рядка або стовпця.
5.                     Обернена матриця та її обчислення.

 

Визначники.

Нехай дано квадратну матрицю другого порядку:

А=.

Визначником (детермінантом) другого порядку матриці А називають число  

() і позначають:     D=detA==.

Приклад

Обчислити визначник другого порядку

detA==2=12+12=24.

Нехай дано квадратну матрицю третього порядку:

А=.

Визначником (детермінантом) третього порядку матриці А називається число

і позначають:

D=detА==.

При обчисленні визначників третього порядку зручно користуватися правилом Саррюса. Покажемо його на схемі:

 

 

Доданки зі знаком «плюс» - це добутки елементів , розміщених на головній діагоналі визначника, і добутки елементів і ,розміщених у вершинах рівнобедрених трикутників, основи яких паралельні головній діагоналі. Зі знаком «мінус» беремо доданки, що є добутком елементів , розміщених на сторонній діагоналі визначника, та у вершинах рівнобедрених трикутників,основи яких паралельні сторонній діагоналі визначника –  ,  .

Приклад   Обчислити визначник третього порядку

detA==3.

 

Властивості визначників.

1. Визначник не зміниться, якщо його рядки міняються місцями з відповідними стовпцями (транспонуються).

Приклад        ==3=2.

2. Якщо поміняти місцями будь-які два рядки (стовпці) визначника, то його знак зміниться на протилежний:

Приклад   =1.

Поміняємо місцями перший і другий стовпці, отримаємо.

=(-2).

3. Спільний множник всіх елементів рядка (стовпця) можна винести за знак визначника.

Приклад

=3,      =-2= -2=-4.

4. Якщо один із рядків (стовпців) визначника складається лише з нулів, то такий визначник дорівнює нулю.
5. Визначник,який має два однакові рядки або стовпці, дорівнює нулю.

Приклад

=1.

6. Визначник,який має два пропорційні рядки (стовпці), дорівнює нулю.

Приклад    =37.

7. Визначник не зміниться, якщо до елементів будь-якого рядка (стовпця) додати відповідні елементи довільного іншого рядка (стовпця), попередньо помножені на деяке число.
8. Визначник трикутної матриці дорівнює добутку елементів головної діагоналі:

 

==.

 

                  Мінори та алгебраїчні доповнення.

Мінором елемента визначника , називається такий новий визначник, який утворюється з даного визначника в результаті викреслювання рядка і стовпця, що містять даний елемент .

Нехай маємо визначник:

.

Мінор ,що відповідає елементу , отримуємо викресливши у визначнику перший рядок і другий стовпець, тобто:

=.

Приклад

Записати мінори , , визначника .

 

=,   =,  =.

 

Алгебраїчним доповненням елемента визначника , називається його мінор , взятий зі знаком . Отже .

Приклад

Записати алгебраїчні доповнення ,, визначника.

 

==4;;=.

 

     Теорема про розклад визначника по елементах рядка або стовпця.

Теорема. Сума добутків елементів будь-якого рядка (або стовпця) визначника на їх алгебраїчні доповнення дорівнює цьому визначнику, тобто

D=+            або             D=.

Ці співвідношення називають розкладом визначника за елементами -го рядка або -го стовпця.

Приклад

Обчислити визначник, розклавши його по елементах 1-го рядка:

 

=3(4+20)-1(-2-0)+2(4-0)=72+2+8=82.

 

                                          Обернена матриця.

Квадратну матрицю А називають не виродженою , якщо її визначник не дорівнює нулю.

Оберненою матрицею до матриці А називають таку, яка в добутку з нею дає одиничну матрицю Е. Тобто .

Теорема. Для того ,щоб квадратна матриця А мала обернену, необхідно і достатньо, щоб матриця А була не виродженою, тобто щоб її визначник не дорівнював нулю.                                            .

                        Правило знаходження оберненої матриці.

1. Знаходять визначники матриці.
2. Знаходять алгебраїчні доповнення всіх елементів    матриці А та записують нову матрицю.
3. Транспонуємо її.
4. Множимо отриману матрицю на .

Приклад      Знайти обернену матрицю до матриці  А=.

Знаходимо визначник:

                             D==2.

Знаходимо алгебраїчні доповнення кожного елемента:   з яких складаємо нову матрицю і  транспонуємо її.

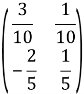
Множимо отриману матрицю на :     =.

Перевіримо отриманий результат. Виконаємо множення  , отримаємо: