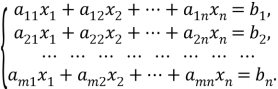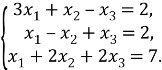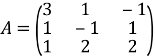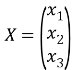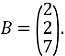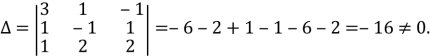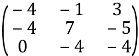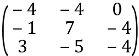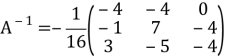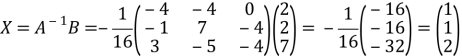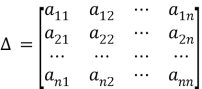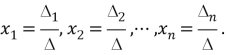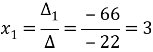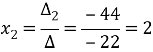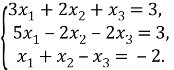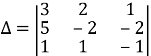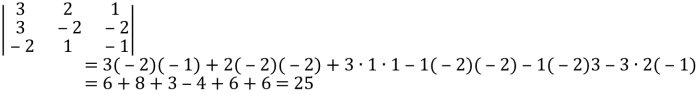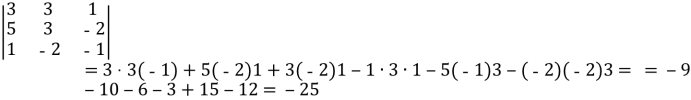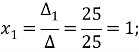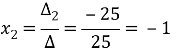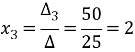Лекція 3

Системи лінійних алгебраїчних рівнянь.

План

1. Системи m лінійних рівнянь з n невідомими.
2. Матричний метод розв'язування систем лінійних рівнянь.
3. Розв'язування систем лінійних рівнянь за формулами Крамера.

 

              Системи m лінійних рівнянь з n невідомими.

Розглянемо систему m лінійних рівнянь, які містять n невідомих.

                               (1)                                                            

Розв’язком системи (1) називається сукупність чисел , що задовольняють усі рівняння системи (1).

Система рівнянь (1) називається сумісною, якщо вона має принаймні один розв’язок, і несумісною, коли вона не має розв’язків.

Система рівнянь (1) називається визначеною, якщо вона має лише один розв’язок, і невизначеною, якщо вона має безліч розв’язків.

Розглянемо дві матриці, які відповідають системі (1):

А називають матрицею системи (1), В – розширеною матрицею системи (1).

Приведемо матрицю В за допомогою елементарних перетворень і відкидання нульових рядків до матриці ступінчастого виду .

Потрібно розуміти, що все, що ми робимо з рядками матриці В, ми робимо з рівняннями системи (1). Тому, очевидно, системи, які відповідають матриці В або   , рівносильні або еквівалентні.

Зрозуміло, що при приведенні В до , матриця А також приводиться до матриці ступінчатого виду, крім випадку, коли останній рядок матриці має вигляд 0 0 0 C, С=0. У цьому випадку, щоб отримати ступінчасту матрицю до матриці А, потрібно відкинути останній рядок. Це означає, що ранг А буде на 1 меншим за ранг матриці В. З іншого боку, коли останній рядок матриці   має вигляд  0 0 0 C, С=0, то це рівносильно тому, що в системі буде відповідне рівняння виду:                           

                                    .

Зрозуміло, що таке рівняння розв’язку не має. Отже, система буде несумісною.

На цій основі доводиться і теорема.

Теорема. (Кронекера-Капеллі). Система (1) сумісна тоді і тільки тоді, коли ранг матриці системи дорівнює рангу розширеної матриці системи.

Якщо rang A = rang B = n, то система визначена, коли rang A = rang B - система невизначена.

Нехай rang A = rang B = .

Якщо  , ( - кількість рівнянь системи), то це говорить про те, що в системі є лише лінійно незалежних рівнянь. Решта рівнянь отримується з тих рівнянь шляхом алгебраїчних перетворень. Такими рівняннями, які лінійно незалежні, будуть саме ті рівнянь, на коефіцієнтах яких можна побудувати визначник порядку, відмінний від нуля. Тільки ці рівняння і потрібно розглядати в системі, решта рівнянь відкидається.

Оскільки в ступінчастій матриці рядків не більше ніж стовпців, то лінійно незалежних рівнянь не може бути більше ніж кількості змінних.

Якщо rang A = rang B =, то система визначена.

Розглянемо випадок, коли rang A = rang B = . Тут виділяють змінних, які називаються головними, а решта  -  змінних називаються вільними. За головні змінні потрібно брати саме ті змінні на коефіцієнтах, при яких можна побудувати визначник   порядку, відмінний від нуля. Таких комбінацій може бути одна або декілька.

Для того, щоб отримати загальний розв’язок системи, потрібно головні змінні виразити через вільні. Розв’язок, отриманий при конкретних значеннях вільних змінних, називається частковим або окремим.  

 

Матричний метод розв'язування систем

Нехай кількість рівнянь системи (1) дорівнює числу невідомих, тобто   m = n. Тоді матриця системи  буде квадратною  , а її визначник  називають основним  визначником системи.

Припустимо, що матриця А невироджена, тобто її визначник  . У цьому разі існує обернена матриця  .

Запишемо систему у матричному вигляді  (2). Помноживши зліва обидві частини матричної рівності на матрицю  , дістанемо:

.

Оскільки , то розв’язком системи буде матриця-стовпець

                                                                     .                (3)

 

Приклад 1.  Розв’язати систему рівнянь матричним методом:

Розв’язання:

Запишемо дану систему у матричному вигляді:

    ,  , 

Спочатку обчислимо визначник цієї матриці:

   

Отже, матриця А невироджена й для неї існує обернена матриця . Обчислимо всі алгебраїчні доповнення матриці :

         

                        

                    

            

        

Складемо нову матрицю:   і транспонуємо її  .

Запишемо обернену матрицю  .

Відповідно .

 

Розв'язування систем лінійних рівнянь за формулами Крамера.

Нехай маємо систему n лінійних рівнянь з n невідомими (1).

Визначник, елементами якого є коефіцієнти при невідомих у системі (1) називається визначником цієї системи і позначається :

                                                        .

Теорема. Якщо визначник системи лінійних алгебраїчних рівнянь (1) відмінний від нуля, то ця система має єдиний розв’язок:

Тут – визначник, утворений з визначника системи (1) заміною -го стовпчика на стовпчик вільних членів.

Розглянемо випадки, коли визначник системи дорівнює нулю.

1. =0 і кожен визначник =0. Це має місце лише тоді, коли коефіцієнти при невідомих пропорційні, тобто кожне рівняння системи отримуємо з першого рівняння множенням обох його частин на деяке число. Очевидно, що при цьому система має безліч розв’язків.

2. =0 і хоча б один з визначників  . Це має місце лише тоді, коли     коефіцієнти при всіх невідомих, крім , пропорційні. Тоді система не має розв’язків. 

Приклад 2.

Розв'язати систему рівнянь за формулами Крамера:

  Розв’язання: Запишемо і обчислимо відповідні визначники:

,           ,        .

Знайдемо значення та за формулами Крамера: 

                             ,       .

Відповідь: , .

Приклад 3.    Розв'язати систему рівнянь за формулами Крамера:

  Розв’язання: Запишемо і обчислимо відповідні визначники:

=3  ;

= ;

=;

=.

Знайдемо значення ,   та за формулами Крамера:

     ;   .

Відповідь: , ,.