Каталог статей
| Головна » Статті » Меню сайту » Вища математика |
|
Лекція 5 Пряма на площині. План
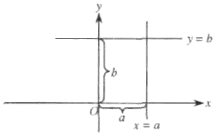
1. Загальне рівняння прямої. Розглянемо на площині прямокутну систему координат і знайдемо рівняння прямої, коли відомий вектор її нормалі n=(А;В) і задано точку Mо(x0;y0) на цій прямій. Нехай М(х;у) — довільна точка шуканої прямої (рис. 1).
За умовою вектор М0М = (х0−x0;y − y0) перпендикулярний до вектора n =(А,В). Тому їх скалярний добуток nМ0М=0. Звідси маємо рівняння A(x-x0) +B(y-y0 ) =0 (1) Це рівняння прямої, яка проходить через дану точку Або Ах +Ву+С=0, С = -Ах0-Ву0.. (2) Це рівняння називається загальним рівнянням прямої. На відміну від рівняння виду (1) змінні х, у входять до рівняння (2) рівноправно. Рівняння (1) завжди можна подати у вигляді (2) Рівняння прямої (2) можна записати у вигляді (у = кх + b) лише за умови В ≠ 0. Коефіцієнти А, В при х, у у загальному рівнянні прямої є проекціями на координатні осі вектора її нормалі n Справджується теорема. Теорема 1. Будь-яка пряма на площині може бути задана лінійним рівнянням виду (2). Кожне лінійне рівняння виду (2), де А2 + В2 > 0, визначає деяку пряму. Доведення. Перше твердження теореми було доведено раніше при виведенні рівняння (1). Доведемо друге твердження. Візьмемо довільне лінійне рівняння Ах + Ву+С=0, А2 + В2>0. Оскільки коефіцієнти при х, у не перетворюються одночасно на нуль, завжди знайдуться значення х x= x0 , y = y0, при яких виконується рівність Ах0 + Ву0 + С = 0. Віднімаючи ці рівняння почленно, дістаємо рівність А(х-х0) + В(у-уо) = 0 (3) За допомогою векторів п=(А,В), М0М = (х-х0, у-у0) рівність (3) можна записати у вигляді nМ0М=0. Як бачимо з рис. 1, вектор М0М тоді і тільки тоді буде перпендикулярним до ненульового вектора n, коли точка М(х, у) лежить на прямій, що проходить через точку М0 (х0,; у0) перпендикулярно до цього вектора. Звідси випливає рівняння (1), що визначає деяку пряму. Отже, теорему доведено. Нехай х, у — координати довільної точки на площині. Пряма (2) поділяє всю площину на дві півплощини. В одній півплощині виконується нерівність Ах + By + С > 0, а в іншій — нерівність Ах + By + С < 0. На самій прямій маємо: Ах + By + С = 0. Розглянемо частинні випадки рівняння (2): якщо А = 0, то пряма паралельна осі х; якщо В = 0, то пряма паралельна осі у; якщо С = 0, то пряма проходить через початок координат; якщо А - 0, С = 0, то пряма збігається з віссю д:; якщо В - 0, С = 0, то пряма збігається з віссю у. Нагадаємо, що пряма проходить перпендикулярно до вектора п = (А,В).
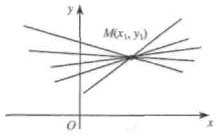
2. Рівняння прямої з кутовим коефіцієнтом. Нехай на площині задано пряму в прямокутній системі координат х, в. Кут ф між віссю Ох і цієї прямої називається кутом нахилу прямій до осі. Тангенс кута нахилу k = tgφ називається кутовим коефіцієнтом розглянутої прямої. Якщо ця пряма перетинає вісь Оу в крапці В с координатами (0;b), то число b називається початковою ординатою. Візьмемо довільну крапку М(х;у) на прямій (мал.2). Якщо розглядувана пряма паралельна осі Оу, то φ = 0,5π і tgφ не існує. При цьому пряма має рівняння виду x=a (рис. 3). З прямокутного трикутника МАВ знаходимо рівняння прямої Рис. 3 Координати х, у будь-якої точки М(х;у), що належить прямій, задовольняють рівняння (1). Якщо пряма (1) проходить через точку M(х;y1), то справджується рівність y1 = kx1+b, Віднімаючи почленно цю рівність від рівності (1), дістаємо рівняння прямої, що проходить через задану точку: у-y1= k(х-х1). (2) Зі зміною кутового коефіцієнта k в рівнянні (2) утворюються різні прямі, що проходять через точку М1 (x1;у1). Рівняння (2) називається рівнянням пучка (в'язки) прямих
| |
| Переглядів: 7218 | |
| Всього коментарів: 0 | |

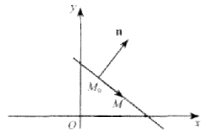
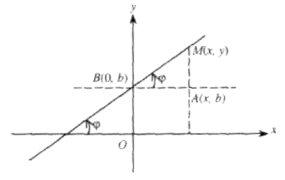 Рис. 2
Рис. 2