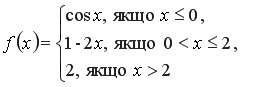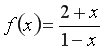НЕПЕРЕРВНІСТЬ І ТОЧКИ РОЗРИВУ ФУНКЦІЇ

Функцію f(x) називають неперервною в точці x0, якщо її границя в цій точці існує і дорівнює значенню функції в цій точці, тобто якщо .

      Якщо функція неперервна в кожній точці , то говорять, що ця функція неперервна на інтервалі .

Значення аргументу, при якому функція не є неперервною, називається точкою розриву функції .

Приклад 1

Дослідити функцію  на неперервність.

Це складна, неелементарна функція. На різних проміжках задана різними аналітичними виразами, кожен із яких є елементарною функцією, а отже, неперервною в своїй області визначення, тому функція може мати розриви тільки в тих точках, де змінюється формула задання функції, тобто в точках та .

 

Таким чином, функція неперервна при , а точка - точка розриву.

Побудуємо графік цієї функції.

 

 

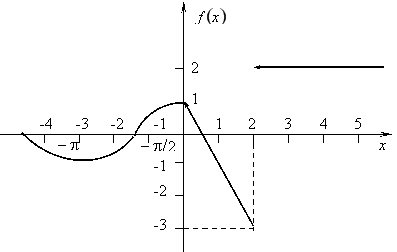
Приклад 2

Дослідити функцію на неперервність.

– це відношення двох многочленів. Вона визначена і неперервна за умови, що знаменник не дорівнює нулю. Оскільки при знаменник дорівнює нулю, то функція в цій точці невизначена, отже, розривна.

 

Приклад 3

Дослідити функцію на неперервність.

Область визначення цієї функції . Отже, в точці функція розривна.

 

Основні властивості неперервних функцій:

1. Алгебраїчна сума скінченного числа неперервних функцій є функцією неперервною.

2. Добуток скінченного числа неперервних функцій є функцією неперервною.

3. Відношення неперервних функцій є неперервною функцією за умови , що знаменник не дорівнює нулю.

4. Складна неперервна функція від неперервної функції є функція неперервна.

5. Перша теорема Вейєрштрасса:

    Якщо функція неперервна на , то вона обмежена

на ,  тобто .

6. Перша теорема Больцано – Коші:

    Якщо функція неперервна на і на кінцях відрізка набуває значень різних знаків, то існує точка , в якій .

8. Друга теорема Больцано – Коші:

   Якщо функція неперервна на , причому , , то для будь-якого числа С, що міститься між і , знайдеться така точка , в якій .

 

 

Приріст аргумента та приріст функції

 

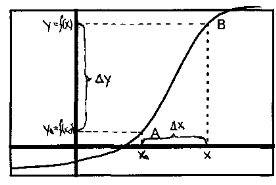
Якщо аргумент функції y=f(x) змінюється від значення х до нового значення хн, то різниця цих значень хн-х називається приростом аргументу і позначають символом .

Сама функція y=f(x) при такій зміні аргумента приймає нове значення ун= f(x+), тобто отримали приріст функції:

                                    = f(x+)- f(x).

 

 

 

 

 

 

Нам потрібно з'ясувати, що таке приріст функції і приріст аргументу. В координатній площині зобразимо графік якої-небудь функції.

Початкове значення х0 збільшилось на якусь величину х - х0 .

В математиці для спрощення величину х-х0 називають приростом незалежної змінної (або аргументу) в т.  х0 і позначають . Говорять, що початкове значення х0 дістало приріст .

Оскільки збільшилось значення аргументу, природно, що буде змінюватись і значення залежної змінної, тобто значення функції. Значення функції змінюється на якусь величину f(x)-f(x0). Цю різницю називають приростом функції  і позначають .

Тепер можна дати ще одне означення неперервної функції:

Функцію f(x) називають неперервною в точці x0, якщо:

•         ця функція визначена в точці x0;
•         приріст функції в точці  x0 прямує до нуля при , тобто   

    .

 

Приклад: Дослідити на неперервність функцію у=х2.

,

отже, функція в точці x0 неперервна.