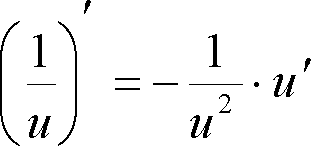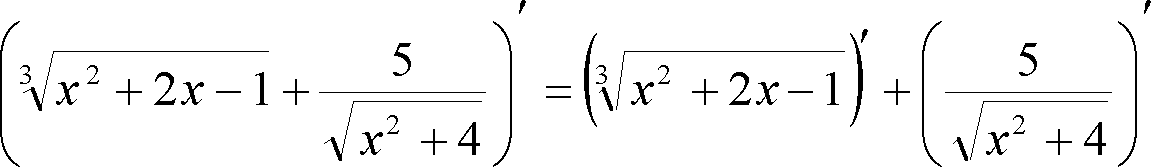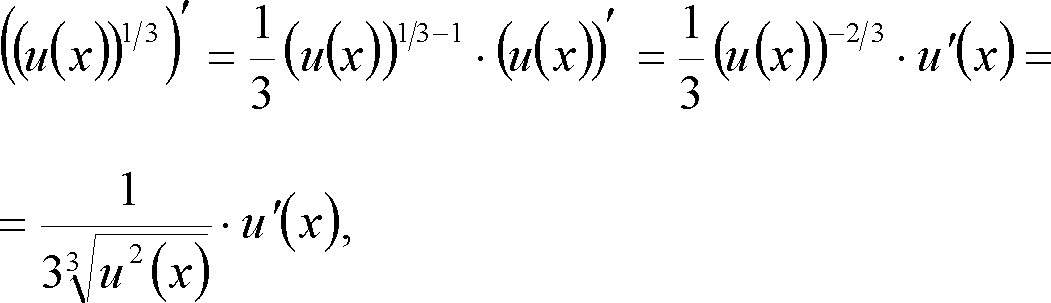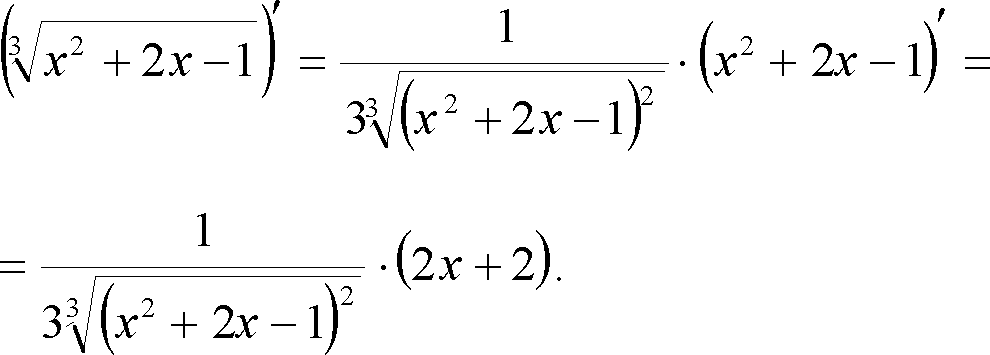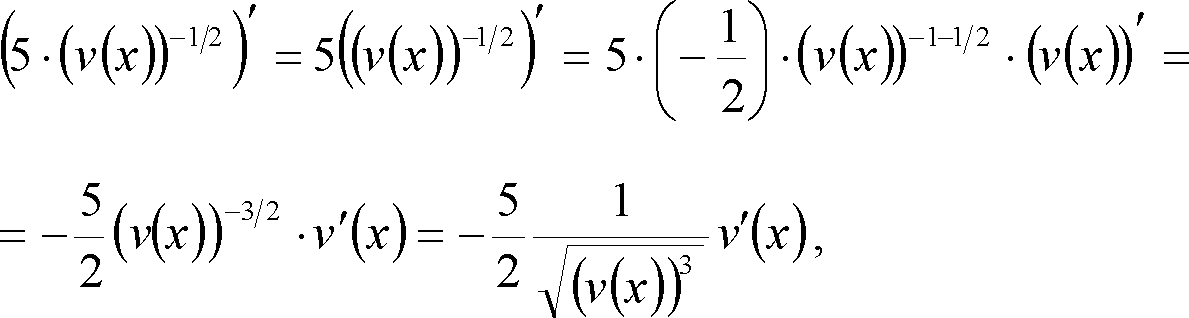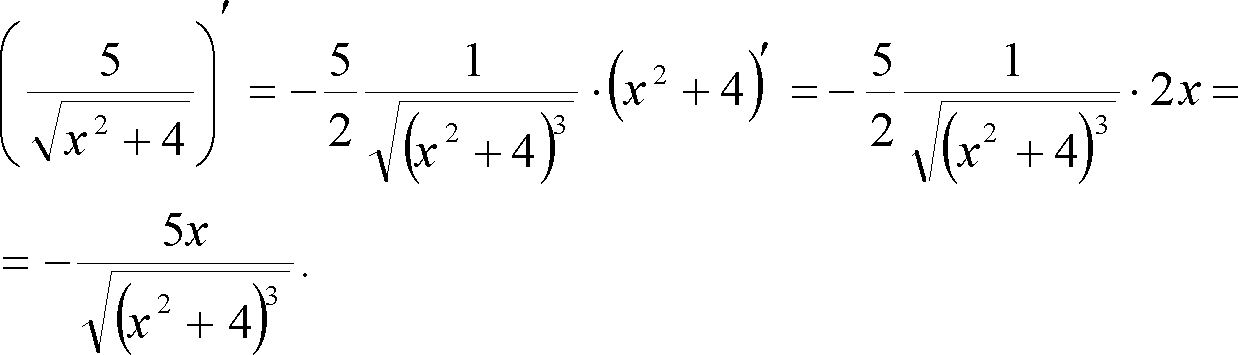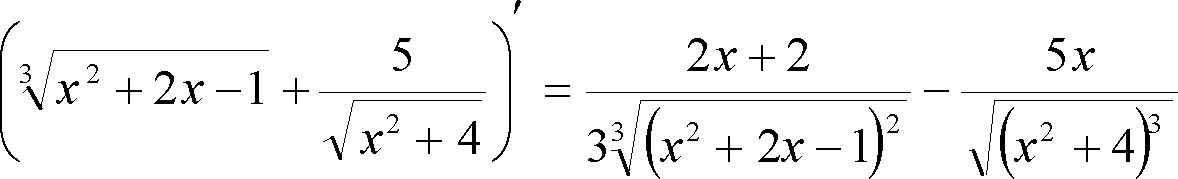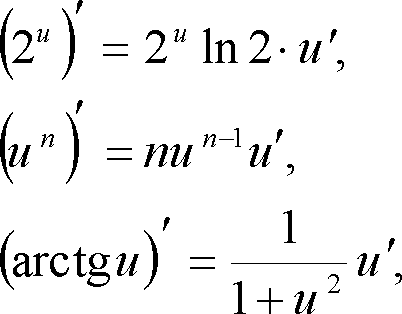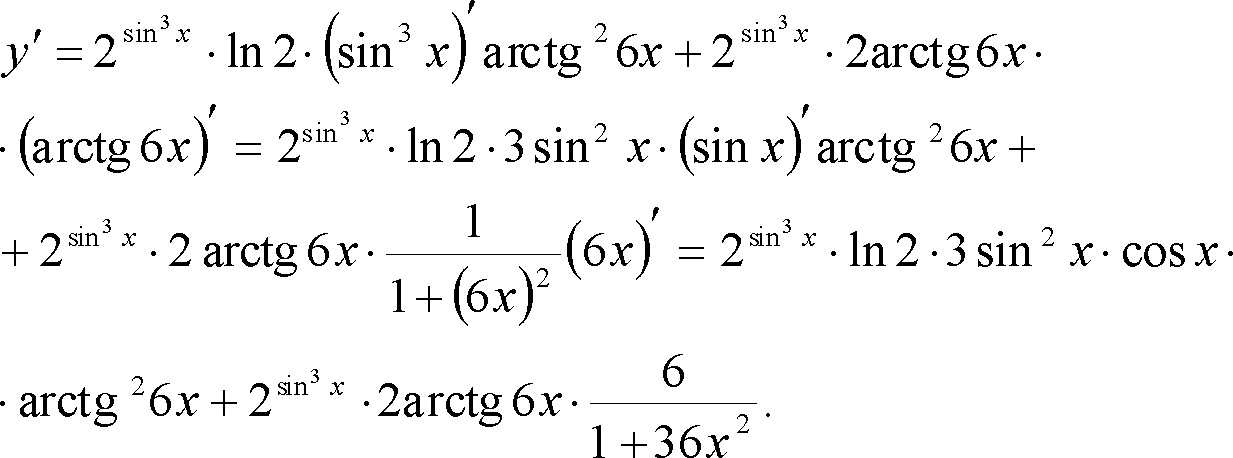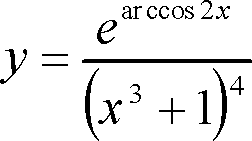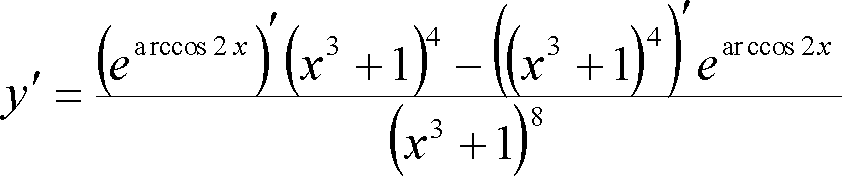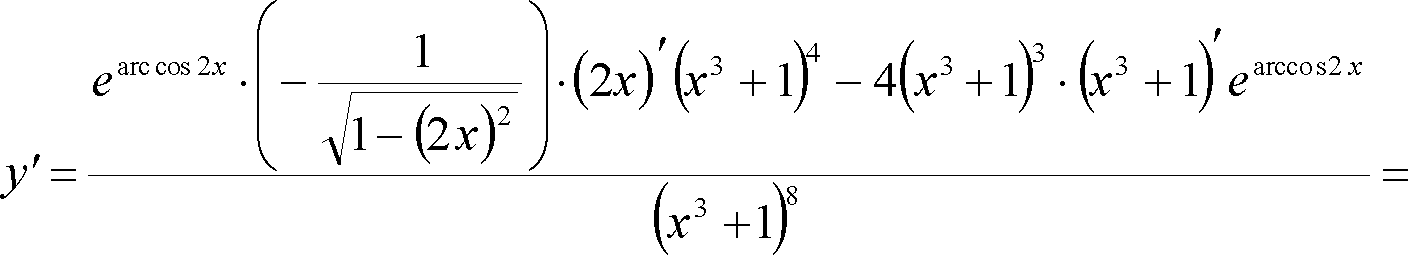Каталог статей
| Головна » Статті » Меню сайту » Похідна та її застосування |
|
ПОХІДНА ФУНКЦІЇ
Нехай функція Якщо існує скінченна границя відношення приросту функції Отже, за означенням Якщо похідна функції Процес знаходження похідної називають диференціюванням. Якщо функція диференційовна в кожній точці Основні правила диференціювання1. Похідна сталої дорівнює нулю, тобто
2. Сталу можна виносити за знак похідної. Якщо
3. Похідна суми дорівнює сумі похідних. Якщо
4. Похідна добутку знаходиться за формулою
5. Якщо
6. Похідна оберненої функції. Якщо функція
7. Похідна складної функції. Якщо Функцію
На основі визначення похідної і правил диференціювання складено таблицю похідних основних елементарних функцій: 1. 3. 5. 7. 9.
Формули диференціювання складних функційВважаємо, що
Досить часто розглядаються похідні таких функцій:
Приклад 1
Приклад 2
Скористаємося таблицею похідних складних функцій. Позначимо
Тоді, скориставшись таблицею похідних, маємо
тобто
Позначимо
тоді
Похідну знаходимо, також скориставшись таблицею похідних:
тобто
Отже,
Приклад 3 Знайти
Треба знайти фактично похідну добутку двох складних функцій (правило 4):
використовуємо таблицю похідних:
Отже,
Знайти
де необхідно знайти похідну частки (правило 5):
Зауважимо, що
Отже,
| |
| Переглядів: 6888 | |
| Всього коментарів: 0 | |

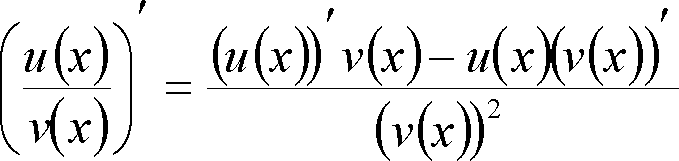
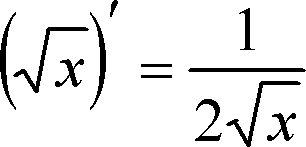 ;
;